2-dimensional p-system

Two-dimensional p-system

Solve the two-dimensional generalization of the p-system:

\[\begin{split}\epsilon_t - u_x - v_y & = 0 \\ \rho(x,y) u_t - \sigma(\epsilon,x,y)_x & = 0 \\ \rho(x,y) v_t - \sigma(\epsilon,x,y)_y & = 0.\end{split}\]

We take \(\sigma = e^{K(x,y)\epsilon} - 1\), and the material coefficients \(\rho,K\) vary in a checkerboard pattern. The resulting dynamics lead to solitary waves, though much more resolution is needed in order to see them.

This example shows how to set an aux array, use a b4step function, use gauges, compute output functionals, and restart a simulation from a checkpoint.

Output:

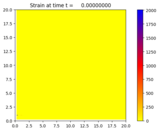
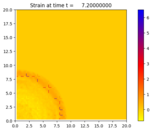
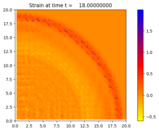
Source:

#!/usr/bin/env python
# encoding: utf-8
r"""
Two-dimensional p-system
==============================

Solve the two-dimensional generalization of the p-system:

.. math:: 
    \epsilon_t - u_x - v_y & = 0 \\
    \rho(x,y) u_t - \sigma(\epsilon,x,y)_x & = 0 \\
    \rho(x,y) v_t - \sigma(\epsilon,x,y)_y & = 0.

We take :math:`\sigma = e^{K(x,y)\epsilon} - 1`, and the
material coefficients :math:`\rho,K` vary in a checkerboard
pattern.  The resulting dynamics lead to solitary waves,
though much more resolution is needed in order to see them.

This example shows how to set an aux array, use a b4step function,
use gauges, compute output functionals, and restart a simulation
from a checkpoint.
"""

import numpy as np
from clawpack import riemann

def qinit(state,A,x0,y0,varx,vary):
    r""" Set initial conditions:
         Gaussian stress, zero velocities."""
    yy,xx = state.grid.c_centers
    stress=A*np.exp(-(xx-x0)**2/(2*varx)-(yy-y0)**2/(2*vary)) #sigma(@t=0)
    stress_rel=state.aux[2,:]
    K=state.aux[1,:]

    state.q[0,:,:]=np.where(stress_rel==1,1,0)*stress/K+np.where(stress_rel==2,1,0)*np.log(stress+1)/K
    state.q[1,:,:]=0; state.q[2,:,:]=0

def setaux(x,y, KA=1, KB=4, rhoA=1, rhoB=4, stress_rel=2):
    r"""Return an array containing the values of the material
        coefficients.

        aux[0,i,j] = rho(x_i, y_j)              (material density)
        aux[1,i,j] = K(x_i, y_j)                (bulk modulus)
        aux[2,i,j] = stress-strain relation type at (x_i, y_j)
    """
    alphax=0.5; deltax=1.
    alphay=0.5; deltay=1.
    
    medium_type = 'checkerboard'

    aux = np.empty((4,len(x),len(y)), order='F')
    if medium_type == 'checkerboard':
        # xfrac and yfrac are x and y relative to deltax and deltay resp.
        xfrac=x-np.floor(x/deltax)*deltax
        yfrac=y-np.floor(y/deltay)*deltay
        # create a meshgrid out of xfrac and yfrac
        [yf,xf]=np.meshgrid(yfrac,xfrac)
        # density 
        aux[0,:,:]=rhoA*(xf<=alphax*deltax)*(yf<=alphay*deltay)\
                  +rhoA*(xf >alphax*deltax)*(yf >alphay*deltay)\
                  +rhoB*(xf >alphax*deltax)*(yf<=alphay*deltay)\
                  +rhoB*(xf<=alphax*deltax)*(yf >alphay*deltay)
        #Young's modulus
        aux[1,:,:]=KA*(xf<=alphax*deltax)*(yf<=alphay*deltay)\
                  +KA*(xf >alphax*deltax)*(yf >alphay*deltay)\
                  +KB*(xf >alphax*deltax)*(yf<=alphay*deltay)\
                  +KB*(xf<=alphax*deltax)*(yf >alphay*deltay)
        # linearity of material
        aux[2,:,:]=stress_rel
    elif medium_type == 'sinusoidal' or medium_type == 'smooth_checkerboard':
        [yy,xx]=np.meshgrid(y,x)
        Amp_rho=np.abs(rhoA-rhoB)/2; offset_p=(rhoA+rhoB)/2
        Amp_K=np.abs(KA-KB)/2; offset_E=(KA+KB)/2
        if medium_type == 'sinusoidal':
            frec_x=2*np.pi/deltax; frec_y=2*np.pi/deltay
            fun=np.sin(frec_x*xx)*np.sin(frec_y*yy)
        else:
            sharpness=10
            fun_x=xx*0; fun_y=yy*0
            for i in range(0,1+int(np.ceil((x[-1]-x[0])/(deltax*0.5)))):
                fun_x=fun_x+(-1)**i*np.tanh(sharpness*(xx-deltax*i*0.5))
            for i in range(0,1+int(np.ceil((y[-1]-y[0])/(deltay*0.5)))):
                fun_y=fun_y+(-1)**i*np.tanh(sharpness*(yy-deltay*i*0.5))
            fun=fun_x*fun_y
        aux[0,:,:]=Amp_rho*fun+offset_p
        aux[1,:,:]=Amp_K*fun+offset_E
        aux[2,:,:]=stress_rel
    return aux

def b4step(solver,state):
    r"""Put in aux[3,:,:] the value of q[0,:,:] (eps). 
        This is required in rptpv.f.
        Only used by classic (not SharpClaw).
    """
    state.aux[3,:,:] = state.q[0,:,:]

def compute_stress(state):
    """ Compute stress from strain and store in state.p."""
    K=state.aux[1,:,:]
    stress_rel=state.aux[2,:,:]
    eps=state.q[0,:,:]
    state.p[0,:,:] = np.where(stress_rel==1,1,0) * K*eps \
                    +np.where(stress_rel==2,1,0) * (np.exp(eps*K)-1) \
 

def total_energy(state):
    rho = state.aux[0,:,:]; K = state.aux[1,:,:]
    
    u = state.q[1,:,:]/rho
    v = state.q[2,:,:]/rho
    kinetic=rho * (u**2 + v**2)/2.

    eps = state.q[0,:,:]
    sigma = np.exp(K*eps) - 1.
    potential = (sigma-np.log(sigma+1.))/K

    dx=state.grid.delta[0]; dy=state.grid.delta[1]
    
    state.F[0,:,:] = (potential+kinetic)*dx*dy 

def gauge_stress(q,aux):
    p = np.exp(q[0]*aux[1])-1
    return [p,10*p]


def setup(kernel_language='Fortran',
              use_petsc=False,outdir='./_output',solver_type='classic',
              disable_output=False, cells_per_layer=30, tfinal=18.):

    if use_petsc:
        import clawpack.petclaw as pyclaw
    else:
        from clawpack import pyclaw

    # material parameters
    KA=1.;   rhoA=1.
    KB=4.;   rhoB=4.
    stress_rel=2;

    # Domain
    x_lower=0.25; x_upper=20.25
    y_lower=0.25; y_upper=20.25
    # cells per layer
    mx=int((x_upper-x_lower)*cells_per_layer)
    my=int((y_upper-y_lower)*cells_per_layer)
    # Initial condition parameters
    initial_amplitude=10.
    x0=0.25 # Center of initial perturbation
    y0=0.25 # Center of initial perturbation
    varx=0.5; vary=0.5 # Width of initial perturbation

    num_output_times = 10

    if solver_type == 'classic':
        solver = pyclaw.ClawSolver2D(riemann.psystem_2D)
        solver.dimensional_split=False
        solver.cfl_max = 0.9
        solver.cfl_desired = 0.8
        solver.limiters = pyclaw.limiters.tvd.superbee
    elif solver_type=='sharpclaw':
        solver = pyclaw.SharpClawSolver2D(riemann.psystem_2D)

    if kernel_language != 'Fortran':
        raise Exception('Unrecognized value of kernel_language for 2D psystem')

    # Boundary conditions
    solver.bc_lower[0] = pyclaw.BC.wall
    solver.bc_upper[0] = pyclaw.BC.extrap
    solver.bc_lower[1] = pyclaw.BC.wall
    solver.bc_upper[1] = pyclaw.BC.extrap
    solver.aux_bc_lower[0] = pyclaw.BC.wall
    solver.aux_bc_upper[0] = pyclaw.BC.extrap
    solver.aux_bc_lower[1] = pyclaw.BC.wall
    solver.aux_bc_upper[1] = pyclaw.BC.extrap

    solver.fwave = True
    solver.before_step = b4step

    #controller
    claw = pyclaw.Controller()
    claw.tfinal = tfinal
    claw.solver = solver
    claw.outdir = outdir
    
    # restart options
    restart_from_frame = None

    if restart_from_frame is None:
        x = pyclaw.Dimension(x_lower,x_upper,mx,name='x')
        y = pyclaw.Dimension(y_lower,y_upper,my,name='y')
        domain = pyclaw.Domain([x,y])
        num_eqn = 3
        num_aux = 4
        state = pyclaw.State(domain,num_eqn,num_aux)
        state.mF = 1
        state.mp = 1

        grid = state.grid
        state.aux = setaux(grid.x.centers,grid.y.centers,KA,KB,rhoA,rhoB,stress_rel)
        #Initial condition
        qinit(state,initial_amplitude,x0,y0,varx,vary)

        claw.solution = pyclaw.Solution(state,domain)
        claw.num_output_times = num_output_times

    else:
        claw.solution = pyclaw.Solution(restart_from_frame, format='petsc',read_aux=False)
        claw.solution.state.mp = 1
        grid = claw.solution.domain.grid
        claw.solution.state.aux = setaux(grid.x.centers,grid.y.centers)
        claw.num_output_times = num_output_times - restart_from_frame
        claw.start_frame = restart_from_frame

    #claw.p_function = p_function
    if disable_output:
        claw.output_format = None
    claw.compute_F = total_energy
    claw.compute_p = compute_stress
    claw.write_aux_init = False

    grid.add_gauges([[0.25,0.25],[17.85,1.25],[3.25,18.75],[11.75,11.75]])
    solver.compute_gauge_values = gauge_stress
    state.keep_gauges = True
    claw.setplot = setplot
    claw.keep_copy = True

    return claw

#--------------------------
def setplot(plotdata):
#--------------------------
    """ 
    Specify what is to be plotted at each frame.
    Input:  plotdata, an instance of visclaw.data.ClawPlotData.
    Output: a modified version of plotdata.
    """ 
    from clawpack.visclaw import colormaps

    plotdata.clearfigures()  # clear any old figures,axes,items data
    
    # Figure for strain
    plotfigure = plotdata.new_plotfigure(name='Stress', figno=0)

    # Set up for axes in this figure:
    plotaxes = plotfigure.new_plotaxes()
    plotaxes.title = 'Strain'
    plotaxes.xlimits = [0.,20.]
    plotaxes.ylimits = [0.,20.]
    plotaxes.scaled = True

    # Set up for item on these axes:
    plotitem = plotaxes.new_plotitem(plot_type='2d_pcolor')
    plotitem.plot_var = stress
    plotitem.pcolor_cmap = colormaps.yellow_red_blue
    plotitem.add_colorbar = True
    
    return plotdata

def stress(current_data):    
    import numpy as np
    aux = setaux(current_data.x[:,0],current_data.y[0,:])
    q = current_data.q
    return np.exp(aux[1,...]*q[0,...])-1.


if __name__=="__main__":
    from clawpack.pyclaw.util import run_app_from_main
    output = run_app_from_main(setup,setplot)