2-dimensional Euler equations¶
Euler 2D Quadrants example¶
Simple example solving the Euler equations of compressible fluid dynamics:
\[\begin{split}\rho_t + (\rho u)_x + (\rho v)_y & = 0 \\
(\rho u)_t + (\rho u^2 + p)_x + (\rho uv)_y & = 0 \\
(\rho v)_t + (\rho uv)_x + (\rho v^2 + p)_y & = 0 \\
E_t + (u (E + p) )_x + (v (E + p))_y & = 0.\end{split}\]
Here \(\rho\) is the density, (u,v) is the velocity, and E is the total energy. The initial condition is one of the 2D Riemann problems from the paper of Liska and Wendroff.
Output:¶
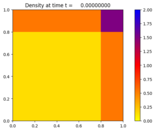
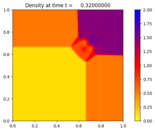
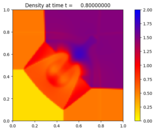
Source:¶
#!/usr/bin/env python
# encoding: utf-8
r"""
Euler 2D Quadrants example
==========================
Simple example solving the Euler equations of compressible fluid dynamics:
.. math::
\rho_t + (\rho u)_x + (\rho v)_y & = 0 \\
(\rho u)_t + (\rho u^2 + p)_x + (\rho uv)_y & = 0 \\
(\rho v)_t + (\rho uv)_x + (\rho v^2 + p)_y & = 0 \\
E_t + (u (E + p) )_x + (v (E + p))_y & = 0.
Here :math:`\rho` is the density, (u,v) is the velocity, and E is the total energy.
The initial condition is one of the 2D Riemann problems from the paper of
Liska and Wendroff.
"""
from clawpack import riemann
from clawpack.riemann.euler_4wave_2D_constants import density, x_momentum, y_momentum, \
energy, num_eqn
from clawpack.visclaw import colormaps
def setplot(plotdata):
r"""Plotting settings
Should plot two figures both of density.
"""
plotdata.clearfigures() # clear any old figures,axes,items data
# Figure for density - pcolor
plotfigure = plotdata.new_plotfigure(name='Density', figno=0)
# Set up for axes in this figure:
plotaxes = plotfigure.new_plotaxes()
plotaxes.xlimits = 'auto'
plotaxes.ylimits = 'auto'
plotaxes.scaled = True
plotaxes.title = 'Density'
# Set up for item on these axes:
plotitem = plotaxes.new_plotitem(plot_type='2d_pcolor')
plotitem.plot_var = density
plotitem.pcolor_cmap = colormaps.yellow_red_blue
plotitem.pcolor_cmin = 0.
plotitem.pcolor_cmax = 2.
plotitem.add_colorbar = True
# Figure for density - Schlieren
plotfigure = plotdata.new_plotfigure(name='Schlieren', figno=1)
# Set up for axes in this figure:
plotaxes = plotfigure.new_plotaxes()
plotaxes.xlimits = 'auto'
plotaxes.ylimits = 'auto'
plotaxes.title = 'Density'
plotaxes.scaled = True # so aspect ratio is 1
# Set up for item on these axes:
plotitem = plotaxes.new_plotitem(plot_type='2d_schlieren')
plotitem.schlieren_cmin = 0.0
plotitem.schlieren_cmax = 1.0
plotitem.plot_var = density
plotitem.add_colorbar = False
return plotdata
def setup(use_petsc=False,riemann_solver='roe'):
if use_petsc:
import clawpack.petclaw as pyclaw
else:
from clawpack import pyclaw
if riemann_solver.lower() == 'roe':
solver = pyclaw.ClawSolver2D(riemann.euler_4wave_2D)
solver.transverse_waves = 2
elif riemann_solver.lower() == 'hlle':
solver = pyclaw.ClawSolver2D(riemann.euler_hlle_2D)
solver.transverse_waves = 0
solver.cfl_desired = 0.4
solver.cfl_max = 0.5
solver.all_bcs = pyclaw.BC.extrap
domain = pyclaw.Domain([0.,0.],[1.,1.],[100,100])
solution = pyclaw.Solution(num_eqn,domain)
gamma = 1.4
solution.problem_data['gamma'] = gamma
# Set initial data
xx, yy = domain.grid.p_centers
l = xx < 0.8
r = xx >= 0.8
b = yy < 0.8
t = yy >= 0.8
solution.q[density,...] = 1.5 * r * t + 0.532258064516129 * l * t \
+ 0.137992831541219 * l * b \
+ 0.532258064516129 * r * b
u = 0.0 * r * t + 1.206045378311055 * l * t \
+ 1.206045378311055 * l * b \
+ 0.0 * r * b
v = 0.0 * r * t + 0.0 * l * t \
+ 1.206045378311055 * l * b \
+ 1.206045378311055 * r * b
p = 1.5 * r * t + 0.3 * l * t + 0.029032258064516 * l * b + 0.3 * r * b
solution.q[x_momentum,...] = solution.q[density, ...] * u
solution.q[y_momentum,...] = solution.q[density, ...] * v
solution.q[energy,...] = 0.5 * solution.q[density,...]*(u**2 + v**2) + p / (gamma - 1.0)
claw = pyclaw.Controller()
claw.tfinal = 0.8
claw.num_output_times = 10
claw.solution = solution
claw.solver = solver
claw.output_format = 'ascii'
claw.outdir = "./_output"
claw.setplot = setplot
return claw
if __name__ == "__main__":
from clawpack.pyclaw.util import run_app_from_main
output = run_app_from_main(setup, setplot)
