1-dimensional Euler equations

Shock-tube problem

Solve the one-dimensional Euler equations for inviscid, compressible flow:

\[\begin{split}\rho_t + (\rho u)_x & = 0 \\ (\rho u)_t + (\rho u^2 + p)_x & = 0 \\ E_t + (u (E + p) )_x & = 0.\end{split}\]

The fluid is an ideal gas, with pressure given by \(p=\rho (\gamma-1)e\) where e is internal energy.

This script runs a shock-tube problem.

Output:

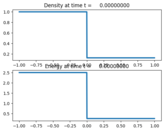
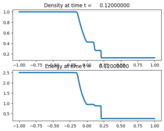
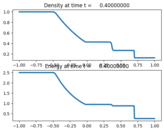
Source:

#!/usr/bin/env python
# encoding: utf-8
r"""
Shock-tube problem
===================================

Solve the one-dimensional Euler equations for inviscid, compressible flow:

.. math::
    \rho_t + (\rho u)_x & = 0 \\
    (\rho u)_t + (\rho u^2 + p)_x & = 0 \\
    E_t + (u (E + p) )_x & = 0.

The fluid is an ideal gas, with pressure given by :math:`p=\rho (\gamma-1)e` where
e is internal energy.

This script runs a shock-tube problem.
"""
from clawpack import riemann
from clawpack.riemann.euler_with_efix_1D_constants import density, momentum, energy, num_eqn

gamma = 1.4 # Ratio of specific heats

def setup(use_petsc=False, outdir='./_output', solver_type='classic',
          kernel_language='Python',disable_output=False):

    if use_petsc:
        import clawpack.petclaw as pyclaw
    else:
        from clawpack import pyclaw

    if kernel_language =='Python':
        rs = riemann.euler_1D_py.euler_hllc_1D
    elif kernel_language =='Fortran':
        rs = riemann.euler_hlle_1D

    if solver_type=='sharpclaw':
        solver = pyclaw.SharpClawSolver1D(rs)
    elif solver_type=='classic':
        solver = pyclaw.ClawSolver1D(rs)

    solver.kernel_language = kernel_language

    solver.bc_lower[0]=pyclaw.BC.extrap
    solver.bc_upper[0]=pyclaw.BC.extrap

    mx = 800
    x = pyclaw.Dimension(-1.0,1.0,mx,name='x')
    domain = pyclaw.Domain([x])
    state = pyclaw.State(domain,num_eqn)

    state.problem_data['gamma'] = gamma
    state.problem_data['gamma1'] = gamma - 1.

    x = state.grid.x.centers

    rho_l = 1.; rho_r = 1./8
    p_l = 1.; p_r = 0.1
    state.q[density ,:] = (x<0.)*rho_l + (x>=0.)*rho_r
    state.q[momentum,:] = 0.
    velocity = state.q[momentum,:]/state.q[density,:]
    pressure = (x<0.)*p_l + (x>=0.)*p_r
    state.q[energy  ,:] = pressure/(gamma - 1.) + 0.5 * state.q[density,:] * velocity**2

    claw = pyclaw.Controller()
    claw.tfinal = 0.4
    claw.solution = pyclaw.Solution(state,domain)
    claw.solver = solver
    claw.num_output_times = 10
    claw.outdir = outdir
    claw.setplot = setplot
    claw.keep_copy = True
    if disable_output:
        claw.output_format = None

    return claw

#--------------------------
def setplot(plotdata):
#--------------------------
    """ 
    Specify what is to be plotted at each frame.
    Input:  plotdata, an instance of visclaw.data.ClawPlotData.
    Output: a modified version of plotdata.
    """ 
    plotdata.clearfigures()  # clear any old figures,axes,items data

    plotfigure = plotdata.new_plotfigure(name='', figno=0)

    plotaxes = plotfigure.new_plotaxes()
    plotaxes.axescmd = 'subplot(211)'
    plotaxes.title = 'Density'

    plotitem = plotaxes.new_plotitem(plot_type='1d')
    plotitem.plot_var = density
    plotitem.kwargs = {'linewidth':3}
    
    plotaxes = plotfigure.new_plotaxes()
    plotaxes.axescmd = 'subplot(212)'
    plotaxes.title = 'Energy'

    plotitem = plotaxes.new_plotitem(plot_type='1d')
    plotitem.plot_var = energy
    plotitem.kwargs = {'linewidth':3}
    
    return plotdata

if __name__=="__main__":
    from clawpack.pyclaw.util import run_app_from_main
    output = run_app_from_main(setup,setplot)