#!/usr/bin/env python
# encoding: utf-8
r"""
Advection-reaction in 2D
========================
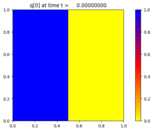
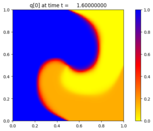
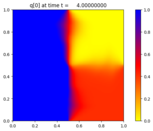
Solve the 2D advection-reaction problem
.. math::
p_t + u(x,y,t) p_x + v(x,y,t) p_y = \epsilon q \\
q_t + u(x,y,t) q_x + v(x,y,t) q_y = \epsilon p
Note that the left hand side of this system is the non-conservative transport
equation for p and q. The Riemann solver assumes that velocities are specified
at cell edges.
This example also shows how to use your own Riemann solver.
"""
import numpy as np
import os
try:
from clawpack.pyclaw.examples.advection_reaction_2d import advection_2d
except ImportError:
this_dir = os.path.dirname(__file__)
if this_dir == '':
this_dir = os.path.abspath('.')
import subprocess
cmd = "make -C "+this_dir
proc = subprocess.Popen("make -C "+this_dir+"/", shell=True, stdout = subprocess.PIPE)
proc.wait()
try:
# Now try to import again
from clawpack.pyclaw.examples.advection_reaction_2d import advection_2d
except ImportError:
raise
t_period = 4.0
epsilon = 0.1
def source_step(solver,state,dt):
"Integrate the source term over one step."
qq = state.q.copy()
state.q[0,:,:] = state.q[0,:,:] + epsilon*dt*qq[1,:,:]
state.q[1,:,:] = state.q[1,:,:] + epsilon*dt*qq[0,:,:]
def psi(x,y):
"Velocity field potential."
return (np.sin(np.pi*x))**2 * (np.sin(np.pi*y))**2 / np.pi
def set_velocities(solver,state):
"Update velocity field for current time."
v_t = np.cos(2 * np.pi * (state.t + solver.dt/2) / t_period)
X, Y = state.grid.p_nodes
dx, dy = state.grid.delta
# u(x_(i-1/2),y_j)
state.aux[0,:,:] = - ( psi(X[:-1,1:],Y[:-1,1:]) - psi(X[:-1,:-1],Y[:-1,:-1]) ) / dy
# v(x_i,y_(j-1/2))
state.aux[1,:,:] = ( psi(X[1:,:-1],Y[1:,:-1]) - psi(X[:-1,:-1],Y[:-1,:-1]) ) / dx
state.aux[:] = v_t * state.aux[:]
def setup(outdir='./_output'):
from clawpack import pyclaw
from clawpack.pyclaw.examples.advection_reaction_2d import advection_2d
solver = pyclaw.ClawSolver2D(advection_2d)
# Use dimensional splitting since no transverse solver is defined
solver.dimensional_split = 1
solver.all_bcs = pyclaw.BC.extrap
solver.aux_bc_lower[0] = pyclaw.BC.extrap
solver.aux_bc_upper[0] = pyclaw.BC.extrap
solver.aux_bc_lower[1] = pyclaw.BC.extrap
solver.aux_bc_upper[1] = pyclaw.BC.extrap
domain = pyclaw.Domain( (0.,0.), (1.,1.), (100,100) )
solver.num_eqn = 2
solver.num_waves = 1
num_aux = 2
state = pyclaw.State(domain, solver.num_eqn, num_aux)
Xe, Ye = domain.grid.p_nodes
Xc, Yc = domain.grid.p_centers
dx, dy = domain.grid.delta
# Edge velocities
# u(x_(i-1/2),y_j)
state.aux[0,:,:] = - ( psi(Xe[:-1,1:],Ye[:-1,1:]) - psi(Xe[:-1,:-1],Ye[:-1,:-1]) ) / dy
# v(x_i,y_(j-1/2))
state.aux[1,:,:] = ( psi(Xe[1:,:-1],Ye[1:,:-1]) - psi(Xe[:-1,:-1],Ye[:-1,:-1]) ) / dx
solver.before_step = set_velocities
solver.step_source = source_step
solver.source_split = 1
state.q[0,:,:] = (Xc <= 0.5)
state.q[1,:,:] = (Yc <= 0.5)
claw = pyclaw.Controller()
claw.tfinal = t_period
claw.solution = pyclaw.Solution(state, domain)
claw.solver = solver
claw.keep_copy = True
claw.outdir = outdir
if outdir == '':
claw.output_format = None
claw.setplot = setplot
return claw
def setplot(plotdata):
"""
Plot solution using VisClaw.
"""
from clawpack.visclaw import colormaps
plotdata.clearfigures() # clear any old figures,axes,items data
# Figure for pcolor plot
plotfigure = plotdata.new_plotfigure(name='q[0]', figno=0)
# Set up for axes in this figure:
plotaxes = plotfigure.new_plotaxes()
plotaxes.title = 'q[0]'
plotaxes.scaled = True
# Set up for item on these axes:
plotitem = plotaxes.new_plotitem(plot_type='2d_pcolor')
plotitem.plot_var = 0
plotitem.pcolor_cmap = colormaps.yellow_red_blue
plotitem.pcolor_cmin = 0.0
plotitem.pcolor_cmax = 1.0
plotitem.add_colorbar = True
# Figure for contour plot
plotfigure = plotdata.new_plotfigure(name='q[1]', figno=1)
# Set up for axes in this figure:
plotaxes = plotfigure.new_plotaxes()
plotaxes.title = 'q[1]'
# Set up for item on these axes:
plotitem = plotaxes.new_plotitem(plot_type='2d_pcolor')
plotitem.plot_var = 1
plotitem.pcolor_cmin = 0.0
plotitem.pcolor_cmax = 1.0
plotitem.add_colorbar = True
return plotdata
if __name__=="__main__":
from clawpack.pyclaw.util import run_app_from_main
output = run_app_from_main(setup,setplot)